理解狄利克雷分布

知乎：深入理解Beta分布

在看一篇有关证据学习的文章时，文中使用了狄利克雷分布，对此很是迷惑，在搜索大量资料后总结了有关狄利克雷的相关知识。希望可以帮助有需要者快速简单理解。本文中主要的论述来自上述链接。

Beta分布

在了解狄利克雷分布之前，首先需要了解Beta分布，因为狄利克雷分布其本质上就是Beta分布的多元表示。因此本文主要介绍Beta分布，以引出狄利克雷分布。

我们都了解二项分布，其中若随机变量 X 付出参数为 n 和 q 的二项分布，则其概率密度函数为

\(
\begin{align}
\begin{split}
p(x)=\begin{pmatrix} n\\ x \end{pmatrix}q^x(1-q)^{n-x}
\end{split}
\end{align}
\)

如果将其看作是关于 q 的函数，即表示某件事件以概率 q 出现成为了一个事件，其本身也具有了概率。此时某种事件已经可以看作是一个已知的固定事件，即 x,n为常数，我们只是在考虑概率的概率。这时将其表述为一个分布为

\(
\begin{align}
\begin{split}
f(q)=kq^a(1-q)^b
\end{split}
\end{align}
\)

其中 a,b 是常数，则对于此时的事件所有概率出现总和应当为1。有

\(
\begin{align}
\begin{split}
f(q)=kq^a(1-q)^b \end{split}
\end{align}
\)

\(
\begin{align}
\begin{split}
\int_{0}^{1}f(q)dq=\int_{0}^{1}kq^a(1-q)^bdq=k\int_{0}^{1}q^a(1-q)^bdq=1 \end{split}
\end{align}
\)

\(
\begin{align}
\begin{split}
k=\frac{1}{\int_{0}^{1}q^a(1-q)^bdq}\
\end{split}
\end{align}
\)

对于Beta分布，通常记为B(a+1,b+1)，这里 +1 我认为只是为了和Gamma函数对应起来更加简洁。

\(
\begin{align}
\begin{split}
B(a+1,b+1)=\int_{0}^{1}q^a(1-q)^bdq, 则
\end{split}
\end{align}
\)

\(
\begin{align}
\begin{split}
k=B(a+1,b+1)^{-1}
\end{split}
\end{align}
\)

\(
\begin{align}
\begin{split}
f(q;a+1,b+1)=B(a+1,b+1)^{-1}q^a(1-q)^b
\end{split}
\end{align}
\)

对其进行改造，使得α=a+1,β=b+1，当q=t时得到Beta函数；当q=x时，得到Beta分布函数

\(
\begin{align}
\begin{split}
B(\alpha,\beta)=\int_{0}^{1}t^{\alpha-1}(1-t)^{\beta-1}dt, 则
\end{split}
\end{align}
\)

\(
\begin{align}
\begin{split}
f(x;\alpha,\beta)=B(\alpha,\beta)^{-1}x^{\alpha-1}(1-x)^{\beta-1}
\end{split}
\end{align}
\)

Beta分布和Gamma函数的关系

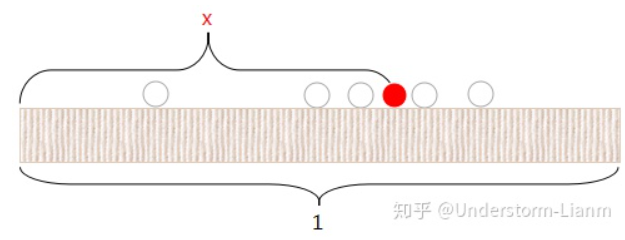beta 假设向长度为1的桌子上扔一个红球，会落在0到1这个范围内，设这个长度值为 x ，再向桌上扔一个白球，那么这个白球落在红球左边的概率即为 x 。若一共扔了 n 次白球，其中每一次都是相互独立的，假设落在红球左边的白球数量为 k，那么随机变量 K 服从参数为 n 和 x 的二项分布。而对于 x 则服从 [0,1] 的均匀分布 X~U[0,1]。对于所有的K和x有

\(
\begin{align}
\begin{split}
P(K=k)=\int_{0}^{1} \begin{pmatrix} n\\ x \end{pmatrix}x^k(1-x)^{n-k}dx= \begin{pmatrix} n\\ x \end{pmatrix}\int_{0}^{1}x^k(1-x)^{n-k}dx
\end{split}
\end{align}
\)

另一种丢球方式，一次性将n+1个球丢出，随机选择一个球作为红球。则任何球被选中的概率为1/n+1。同样，红球左边有0，1，…，n个球的概率也是 1/n+1。（第一个球被选中=左边有0个球，第二个球被选中=左边有1个球，…，第n+1个球被选中=左边有n个球）此时有

\(
\begin{align}
\begin{split}
P(K=k)=\int_{0}^{1} \begin{pmatrix} n\\ x \end{pmatrix}x^k(1-x)^{n-k}dx \\= \begin{pmatrix} n\\ x \end{pmatrix}\int_{0}^{1}x^k(1-x)^{n-k}dx=\frac{1}{n+1}\
\end{split}
\end{align}
\)

\(
\begin{align}
\begin{split}
\int_{0}^{1}x^k(1-x)^{n-k}dx=\frac{(n-k)!k!}{n!}\frac{1}{n+1}=\frac{k!(n-k)!}{(n+1)!}\
\end{split}
\end{align}
\)

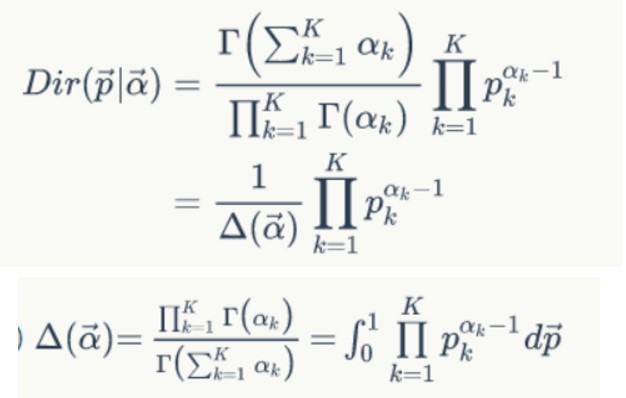而Gamma函数的定义是

\(
\begin{align}
\begin{split}
\Gamma(m)=\int_{0}^{+\infty}e^(-x)x^{m-1}dx=(m-1)!\
\end{split}
\end{align}
\)

令 k=α-1,n-k=β-1，即n=a+b-2，可得到

\(
\begin{align}
\begin{split}
B(\alpha,\beta)=\int_{0}^{1}t^{\alpha-1}(1-t)^{\beta-1}dt=\frac{(\alpha-1)!(\beta-1)!}{(\alpha+\beta-1)!}
\end{split}
\end{align}
\)

\(
\begin{align}
\begin{split}
B(\alpha,\beta)=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)!}
\end{split}
\end{align}
\)