本文介绍决策智能实验室和河口海岸国重合作的AI4Ocean的工作——海洋有效波高估计。
作者: 李哲, 徐榕荟, 胡吉林, 彭忠, 卢玺, 郭晨娟, 杨彬
关键词: 海洋有效波高预测, 大语言模型, 提示微调
摘要: 有效波高(SWH)是海洋科学中的一个重要指标,可以显著反应海洋波浪变化,对全海域SWH进行准确估算是至关重要的。传统数值模型在处理SWH估算任务中虽然具备成熟理论基础,但存在计算效率低下和难以进一步提高的问题。虽然,机器学习技术为解决上述问题提供新的可能性,但由于有限的观测技术和高昂的观测成本,实际观测到的海洋数据的严重稀缺,限制了机器学习模型的潜力。因此,我们提出了一个海洋SWH估算框架(Orca)。具体来说,Orca通过所设计的提示模板实现LLM在SWH估算任务上的迁移,使用一种新的时空感知编码模块增强了传统大语言模型(LLM)的时空推理能力。最终通过大量实验证明了Orca在SWH估算中取得了SOAT且高效的性能。
1. 引言
有效波高(Significant Wave Height, SWH)是海洋科学中的一个重要指标,反映了海洋活动的状态。异常波浪会对人类社会和自然环境造成严重破坏,包括生产损失、人员伤亡和生态损害等。因此对海洋SWH的准确估算关系到各类海上活动的安全,如海上导航、渔业运输和海洋能源开发等。
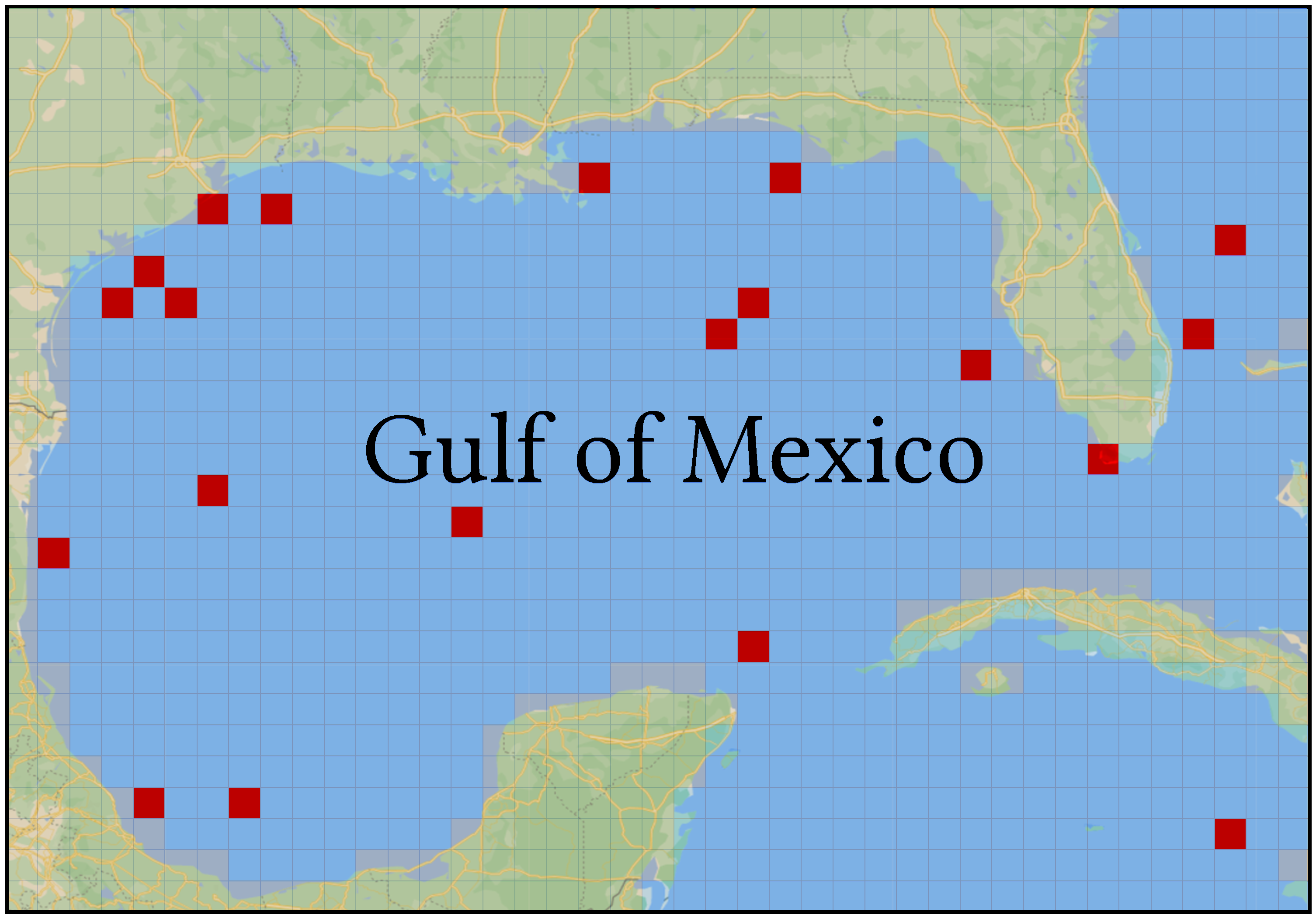
目前SWH估算的方法主要分为两类:传统的数值模型方法和基于机器学习的方法。数值模型基于物理学理论构建,通过利用观测数据推演海洋波浪的所有变化实现对全海域SWH的估算。经过多年的研究积累,数值模型已经具备坚实的理论基础和准确性。但对海洋波浪变化的所有可能性的推演往往需要大量计算资源,且难以适应新的影响因素,模型性能过于依赖物理理论。因此,基于机器学习的方法已经成为一种很有前途的替代方法,在SWH估算中提供了更好的准确性和更少的计算时间。然而,同时也面临着两个主要的挑战:一方面,实际观测的SWH数据过于稀疏。由于观测技术、观测环境以及观测成本的限制,海洋中实际部署的观测浮标非常稀少,如图1显示了墨西哥湾浮标的分布。这种稀缺性阻碍了基于机器学习的方法的发展。另一方面,波浪的产生是不同方向多种力的相互作用,因此波的变化具有很强的时空相关性,但目前基于机器学习的方法未能捕捉到如此复杂的关系。
为了解决上述两个挑战,我们提出了一个海洋SWH估算框架——Orca。具体来说,首先,由于大型语言模型(Large Language Model, LLM)在不同领域小样本场景下展现出了强大的泛化能力,我们以LLM作为模型主干,通过特定的提示模板和嵌入模块实现LLM的迁移,解决SWH估算中的数据稀疏性问题。其次,为了增强LLM的时空推理能力,我们将基于浮标的数据分割成重叠的补丁,通过一种新的时空编码模块捕捉海洋波浪的时空信息。同时,我们通过正则化项增加数值模型的物理知识对模型估算的约束。Orca整合了数值模型和机器学习模型的优点,弥补了LLM时空推理能力的不足,为海洋SWH估算提供新的方向。
综上所述,我们在本文中做出以下贡献:
- Orca是第一个将LLM引入海洋SWH估算的模型。
- 我们设计了一个特定的提示模板和提示嵌入模块,通过有限数据对LLM进行微调,解决了数据稀疏问题。
- 我们提出了一种新的时空感知编码模块,补足了LLM的时空推理能力。
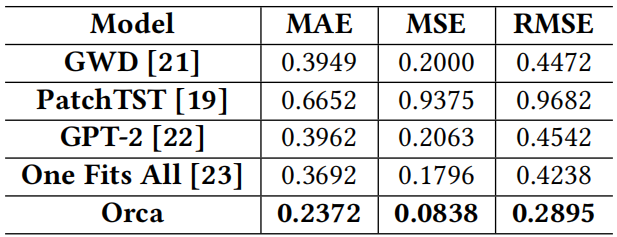
- 进行了大量的实验,证明了Orca的计算效率和准确性。
2. 定义
-
有效波高(SWH): 在给定区域的一组波中,最高1/3波浪的平均高度。
-
基于浮标的数据: $M$个固定在不同位置的浮标在$T$个连续时间间隔中收集到的$F$种观测变量序列,记作$\mathbf{X} \in \mathbb{R}^{F \times M \times T}$。
-
基于网格的有效波高(GSWH): $T$个连续时间间隔内每个网格区域内的平均SWH,记作$\mathbf{Y}\in \mathbb{R}^{K \times J \times T}$,其中$K$和$J$分别表示行数和列数。
-
问题定义 给定在$T$个连续时间间隔的基于浮标的数据X,估算对应时间的GSWH值$Y$。
3. 方法
图2给出了Orca的总体架构。模型一共包含三个模块:提示编码模块、时空感知编码模块、大语言模型。具体来说,设计提示模板,描述大语言模型扮演角色、任务目标、数据格式等信息,为大语言模型在此任务上的微调进行精确的方向定位;将一定时间段的浮标数据作为输入,通过时空感知编码模块学习浮标数据的时空表征;而对于大语言模型本身,冻结包含了大量预训练知识的前馈层和注意力机制模块的参数,只对输入表征的位置编码层的参数进行训练,通过线性层将大语言模型最后的隐藏层的输出映射为预测目标。
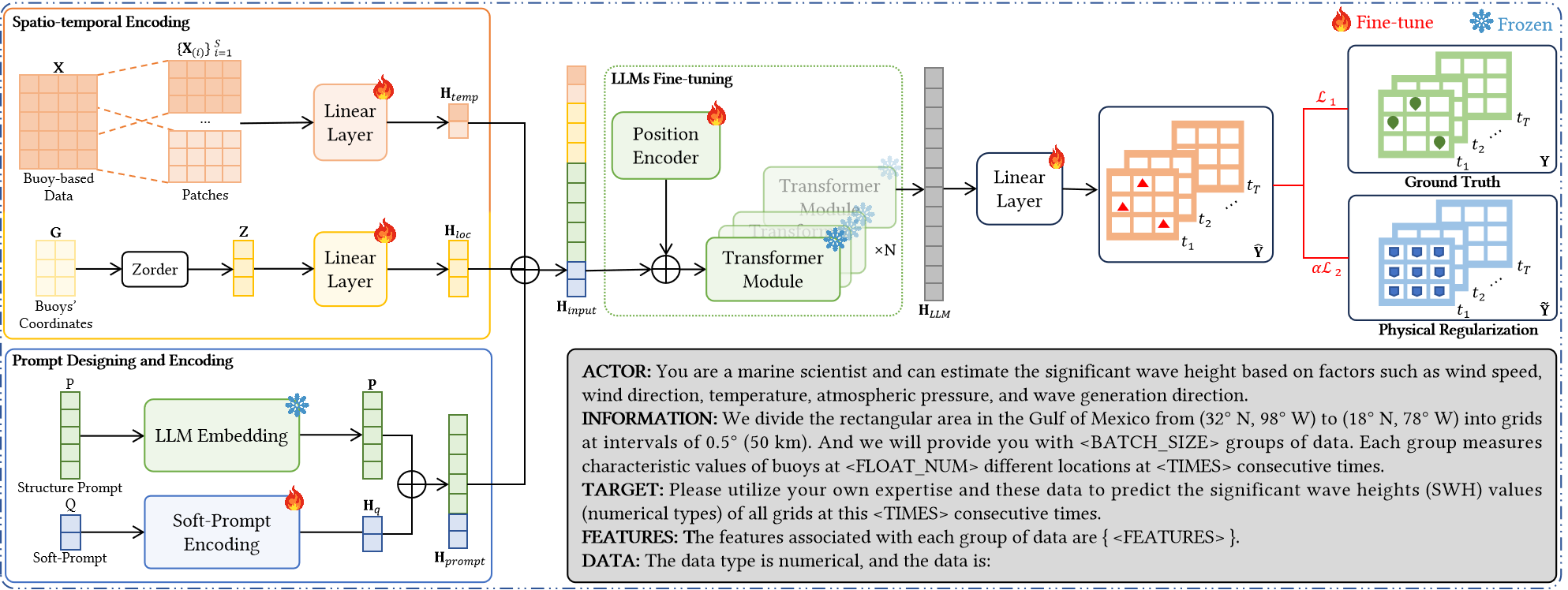
3.1 提示编码模块
为了指导LLM准确地理解数据,我们将提示符分割成五个不同的组件,如图2所示:ACTOR指定LLM的角色;INFORMATION定义输入数据的维度;TARGET明确说明任务目标;FEATURES指定输入数据的特征,如风向(WDIR);DATA声明输入数据的类型,确保LLM准确地解释数值,而不是将它们误认为字符串。
使用LLM的词嵌入层对输入的结构化提示 $P={p_1, p_2, \ldots, p_E}$ 进行编码,得到 $\mathbf{P}={\mathbf{p}_1, \mathbf{p}_2, \ldots, \mathbf{p}_E}$ 。同时,随机生成固定数量的软提示 $Q={q_1, q_2, \ldots, q_R}$... read more
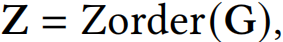
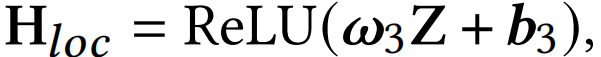
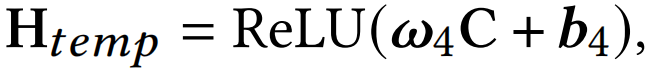
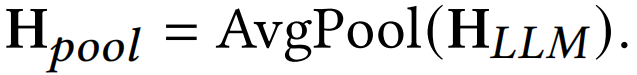
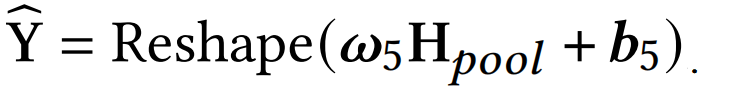
 </ditv>
</ditv>
评论